Parallel Traversal of a Skeletal Animation Tree

Intro

In this post, I want to show a way to iterate a skeletal animation tree in a faster way but before jumping to the actual way of showing this, I will review a few topics like skeletal animation and tree node indexing  as a prelude to the topic.

Skeletal Animation Representation

Skeletal animation is represented by a tree data structure usually called skeleton though the name can be different based on the animation platform you are using. For instance in OGRE3D or Unreal Engine is called skeleton. For the sake of simplicity, I also call it skeleton in this post.

Skeleton tree is an abstract representation of a body of a human or an animal. This abstract representation can describe the relationship between the bones exactly like the way a human or an animal body is. For instance the elbow joint is connected to upper arm. When upper arm moves the elbow is taking the upper arms motion so we can say the elbow is the follower of upper arm. Such relationship can be defined by a parent-child schema and a tree data structure is a very good way to show a set of parent-child relationship for all the bones of the body. That's why a skeleton in animation is literally a tree structure!

For the skeletal animation, each node of the tree is called bone or sometimes joint. I will call them bones in this post to unify the vocabulary. Bones hold a 3D transformation which are passed to the skinning modifiers to move the mesh's vertices and animate the mesh of the characters.

Indexing the tree nodes

Now that we have a tree representing the skeleton, we should be able to traverse the tree and process the nodes upon any need. So the question here is that which method of tree indexing you need to take?That's a very important question for an animation system to answer because it has an influence on the performance of an animation system. The most common ways of indexing tree nodes are pre-order, post-order, in-order and level-order. I haven't seen post-order and in-order anywhere being used in any animation system I worked on and I don't see it being beneficial to be used for traversing a skeleton but level-order and pre-order are common to be used and they work well for animation. To select a good tree indexing method you need to have these points in mind:

1- How to specify each bone's parent?

2- How to specify each bone's children?

3- For world/modeling space calculation of the bones where you need to access the parent or children of each bone, there should be small amount of jumps in memory.

4- Does the tree indexing method allow you to process the tree in parallel?

Now let's just focus on pre-order and level-order tree traversal and decide which one to pick for our tree indexing method. Before going forward, take a look at these two photos showing tree indexing for pre-order and level-order tree traversal:

The tree indices shows the order of processing of the tree nodes (bones). In case of animation, we are most likely processing their 3D transformation so a fairly simple linear algebra operations!

Before comparing pre-order and level-order, I would like to point out that I'm forming the whole tree nodes in a flat array of transforms, where each array index represents the bone index. For instance, array element at index 10 represents the bone with index 10 and the element is just holding position, rotation or scale. When processing the animation data, most of the times we don't even care for the hierarchy. For instance when blending between two poses in local(parent) space, we just need to read the transforms of the same bone indices between two transform array and blend them together so no hierarchy checks are involved. This was said to explain why we just keep a flat array of transforms to represent a skeleton tree. This way of representing a tree is different than what is usually shown for tree structures in academic books. In academic materials, it's very often to make trees using linked lists, connecting the nodes with newly allocated nodes through pointers. This way of showing a skeleton tree won't work well for a real-time animation systems due to lower degree of locality of references. Real-time animation systems should run efficient and fast, not wasting unnecessary CPU cycles. So in order to have the data representing the hierarchy, we define other flat arrays showing the children and parents of each tree node. We can refer to these arrays whenever we need to have access to the hierarchy data. This array's elements keep the data of parent and children of the bone at the current bone index. For instance element 10 of these arrays keep the parent index and children indices of the bone with index 10.

Now let's get back to the 4 points above to compare pre-order and level-order tree traversal methods.

1- How to specify each bones's parent? For both the level-order and the pre-order, the parent index can be just defined by one index in our skeleton tree hierarchy data. So both methods are equal in this case.

2- How to specify each bone's children? Level-order absolutely wins this as specifying children of each bone can be defined by only two indices. One showing first child index and one last child. Any other children has an index between first and last child. If you look at the image of level-order indexing at the beginning of the post, the children of each bone are arranged sequentially. This is not true for the pre-order. To specify the children of each bone in pre-order tree indexing, we need to define an array of indices showing the children of each node. This brings some difficulty and extra data to handle for each node. Also this means accessing the children nodes ends up with possible memory gather and scatters.

3- For world/modeling space calculation of the bones where you need to access the parent or children of each bone, there should be small amount of jumps in memory: 

When using pre-order, there is a notable chance that the parent bone of each bone is the bone with  the previous index especially for the bone structures like spine, neck and finger joints so the locality of references for some bone structures like spine, neck and finger joints is high. This is not necessarily true for the level order as the bones are indexed based on the level so memory location differences are more often between parent and child bones. We can say accessing the parents in pre-order in average has a higher degree of locality of references compared to level order.

On the reverse, in the level-order traversal, the children of each bone are always next to each other in memory so accessing children of each bone should be done without memory jumps. This is not true in pre-order as the children are scattered around. For processing the whole skeleton tree in cases like world/modeling space calculations or branch filtering, you need to have access to both parent and children and level-order works better in such cases in average.

4- Does the tree indexing method allow you to process the skeleton in parallel? Level-Order does! I will explain this in the next sections.

Level-Order Traversal Representation

So with the reasoning done in the past section, I pick level-order for the skeleton tree traversal method. I define the skeleton tree with three flat array with element numbers equal to the skeleton bone count (BonePositions, BoneRotations and BoneScales).

I also define the skeleton tree hierarchy data as structure of array called BoneIndexDataSOA. Each array element show the parent, first child or last child of the bone. If the bone has no child, value of -1 is used.

struct BoneIndexDataSOA
{
    std::vector<int> Parents;
    std::vector<int> ChildrenStart;
    std::vector<int> ChildrenEnd;
};
//
__declspec(align(16))
struct BoneData
{
    float X = 0.f;
    float Y = 0.f;
    float Z = 0.f;
    float W = 0.f;

    inline BoneData operator+(const BoneData Other)
    {
        BoneData Ret;
        Ret.X = X + Other.X;
        Ret.Y = Y + Other.Y;
        Ret.Z = Z + Other.Z;
        Ret.W = W + Other.W;
        return Ret;
    }
};

//
std::vector<BoneData> BonePositions;
std::vector<BoneData> BoneRotations;
std::vector<BoneData> BoneScales;
BoneIndexDataSOA BonesMapSOA;

Parallel Traversal of a Skeleton Tree 

We already picked level-order skeleton tree indexing and defined the structures to represent it. Now what if we boost the tree traversal method and process the bones in parallel? When we traverse the tree, we do some operation on each tree node. For instance for calculating the modeling space transformation of a skeleton, the process on each bone is the multiplication of the bone transformation and its parent. So now we want to see if we can process these operations in parallel. By parallel processing it means we process more than one bone at a time.

Such a thing is possible with SPMD programming and level-order traversal is a good suit for it. To handle the SPMD programming I used Intel ISPC compiler. It is an implicit SPMD programming compiler but a very powerful one!

We're going to parallel process the children of each bone. Since the children of each bone are located sequentially in the memory, we can utilize the usage of ISPC as ISPC eventually map the program indices into SIMD registers (as it's an implicit SPMD). So sequential memory means easier vector load/store in which ISPC is great at.

Below I defined three functions to compare the performance with. Two are traversing the skeleton using MSVC with serial code execution and one using ISPC with parallel code execution. Our operation on each bone is to add the position of each bone with its parent. A fairly simple operation!

//Calculating the sum of each bone position with its parent using level-order traversal

void LevelOrderSum()
{
    for (int I = 0; I < BonePositions.size(); I++)
    {
        if (BonesMapSOA.ChildrenStart[I] != -1)
        {
            for (int J = BonesMapSOA.ChildrenStart[I]; J <= BonesMapSOA.ChildrenEnd[I]; J++)
            {
                BonePositions[J] = BonePositions[J] + BonePositions[I];
            }
        }
    }
}

// Traversing the tree in a faster way only by querying the parent.

// This runs faster than LevelOrderSum due to less condition checks.

// It's a tree traversal-agnostic method.

// It just needs the access to the parent index however it's not possible to use this method-

// for implicit SPMD programming.

void RegularTraverseSum()
{
    for (int I = 1; I < BonePositions.size(); I++)
    {
        BonePositions[I] = BonePositions[I] + BonePositions[BonesMapSOA.Parents[I]];
    }
}

// ISPC function. Parallel processing of the children of each bone using-

// implicit SPMD programming by utilizing the SIMD commands and registers.
export inline void ParallelLevelOrder(const uniform int InChildrenStart[], const uniform int InChildrenEnd[], uniform float OutData[], const uniform int BonesCount)
{
    for (uniform int I = 0; I < BonesCount; I++)
    {
        if (InChildrenStart[I] != -1)
        {
            foreach(J = InChildrenStart[I]...InChildrenEnd[I] + 1)
            {
                OutData[J] += OutData[I];
            }
        }
    }
}

Now I compare the time each function takes to run. Note that all the functions provide the same output and only the execution time is different.

For comparison I defined a tree of 40000 bones and processed it 100 times. Here are the results:

LevelOrderSum: 6.3 milliseconds

RegularTraverseSum: 4.374 milliseconds

ParallelLevelOrder: 1.795 milliseconds

As seen above, the parallel processing using ISPC compiler runs much faster than the serial C++ codes however the comparison is not yet fair!

When I defined the + operator on BoneData struct, I didn't vectorize the + operation. In a game/graphics engine,  all these vector operations are using SIMD commands so it's not fair not to use the SIMD commands for our comparison. To make the results closer to reality, I change the BoneData struct like this:

struct BoneData
{
    __m128 Data = _mm_setzero_ps();
    inline BoneData operator+(const BoneData Other)
    {
        BoneData Ret;
        Ret.Data = _mm_add_ps(Data, Other.Data);
        return Ret;
    }
};

So now we can check the results in a more fair comparison:

LevelOrderSum: 3.93 milliseconds

RegularTraverseSum: 2.65 milliseconds

parallel_level_order: 1.795 milliseconds

The first two functions improved a lot almost twice better but still not as good as the result with parallel processing. In a  nutshell, ISPC utilized the usage of SIMD registers and since my local PC is supporting AVX2, it serialized each bone's children positions in ymm registers and at least processes two vectors at the same time while the + operator above only processes one vector. This degree of parallelism can grow even more if your CPU supports AVX 512!

Why Pre-Order Is Not Suitable for Parallel Skeleton Processing?

There were two reasons that we could parallel process the children of each bone in the skeleton efficiently, one is that the children are sequentially allocated in memory and second is that when we are writing to the children transforms, the parent transform is already written and we just read it. So we can say there is a sequence point between reads and writes here but this is not true if we want to parallel process the bones using pre-order indexing! In pre-order, when we serialize the sequential bone indices to be loaded into the SIMD registers, there is a big chance we are processing the parent and child transforms at the same time which means we are reading the parent transform to calculate the child transform while the parent is being written itself so there can be race over the data.

However we can traverse the pre-order indexed skeleton in a different way by introducing memory gather and scatters but that might not end up efficient so I skip talking about that here.


Is Parallel Processing a Skeleton Tree Always a Win?

Such win in parallel processing of a skeleton usually shows up if you have characters with many bones. Especially characters with loads of muscle correctives and facial joints. It might not be a win for the characters with simple hierarchies including only big muscles!

OGRE3D Animation System

I finished writing my bachelor of science project more than 11 years ago. This was almost the time I was finishing my first video game project called Garshasp: The Monster Slayer with company "Dead Mage".

At that time the company was developing their own in-house engine based on OGRE3D open source graphics engine. At the same time that I was working with Dead mage on Garshasp, I tried to totally learn and understand the animation system of OGRE3D so I dedicated my Bachelor project on totally understanding the animation system of OGRE3D and as a result implemented an animation layering system on top of it.

Here I put the full document of the project. This can give you a good understanding of an animation system from scratch. Of course the user base of OGRE3D has dropped much lower after public release of engines like Unity and Unreal Engine but the purpose here is to get familiar with the basics of an animation system architecture.

Sorry, the text is only in Persian so it can be only useful for Persian speaking game developers.

Animation Layering System on Top of OGRE3D

How To Implement Active Ragdoll

You might have seen video game characters getting hit by a bullet or an explosion and turn into ragdoll while ending up in a pose very similar to animated pose where they can blend back smoothly to the animation! In this post I try to show you how you can implement an active ragdoll to drive the joint motors toward the animation pose to achieve this goal. I've already written another post which was targeting how to use these kind of systems, if you already have them implemented. You may want to check it out too:

Combing Ragdoll and Keyframe Animation to Achieve Dyanmic Poses

So this post focuses on implementing such systems and it comes with required source code. Source codes here are written for Unreal Engine 4. Before going forward you might know that UE4 already supports active ragdoll as an engine feature and you don't really need to reimplement it. This post just carries an academic approach to let the developers know how these kind of systems are implemented in general. To find out how UE4's physically based animation works you can watch this nice video tutorial:

How To Make An Active Ragdoll / Unreal Engine 4

Physically based animation is also known as active ragdoll or animation driven ragdoll and if you have used Havok animation before, it's called powered ragdoll in Havok animation. In this article I call it active ragdoll implying on a ragdoll simulated character trying to follow animation poses(s).


How Does An Active Ragdoll Work?

So imagine you have setup your character with joint constraints and motors and it can simulate as a ragdoll on collisions. Your goal is to make the ragdoll following an animation pose while making the body still reacting to external physical forces and avoid having a loose physical pose.

To solve this problem, let's consider a simple case for just one bone. While you setup your character for ragdoll simulation, a rigid body should be attached to the bone to represent its physical properties like volume, mass, friction etc. The movement of this physical body is controlled by a physical constraint and a motor attached to it. So the angular and linear velocity of the bone is controlled and limited by the constraints it's assigned to. Now imagine you just do a normal ragdoll simulation without following any animation. When you run the simulation the bone as a rigid body gains some angular and linear velocity and based on these velocities the rigid body moves in space!

Now you know that we have angular and linear velocities for bones then we can control these velocities to adjust the physical body to follow the animation easily. To move the ragdoll toward the animation, we can have access to the rotation of the rigid body attached to bone (it's last frame rotation). We can also get the rotation of the bone from animation pose and we have access to the frame's delta time! The difference between the rotation of the bone from animation and the rigid body's simulated rotation from last frame shows how much we should rotate our bone in this frame. We can get the rotation axis of this difference rotation (in quaternions) and scale its length by the angle of the quaternion representing this rotation divided by delta time. We do this length scale because angular velocity is defined by a vector which its direction shows the rotation direction and its length represents angular speed.

This angular velocity can rotate the bone from its current rotation to the pose provided by animation because it rotates the bone from its current rotation to the rotation coming from animation pose in current frame's delta time. Just note, the animation should have been updated at this point to be sure  we're receiving this frames's valid animated pose but physics should be updated afterwards to avoid having one frame delay. Because we get the animation pose and then set the physics velocity and then we want to run the simulation so these calculations should be done before physics loop and after animation update or after certain pose update of animation like an animation node.

Same calculations can be done for bone's linear velocity. We just need to use bones's translation instead of rotation in this case and of course we need to work with vectors instead of quaternions. Applying linear velocity is helping the character to follow the animated bones' positions as well which can be used for bones carrying translation keyframes like pelvis.

If we do this procedure for all the bones in the skeleton hierarchy, we can be sure all the rigid bodies will exactly follow the animation pose. The bones velocity can still be changed because of the external physical forces applied to them from physics world. So this is the point that the bone can still react to external forces while trying to follow the pose from animation. You can find all the codes I've written for this case here. I provided an animation node handling the subject. Note that the skeletal mesh should be physically simulated to see the effect:

Header here:

#pragma once

#include "Engine.h"
#include "AnimGraphNode_Base.h"
#include "Runtime/Engine/Classes/Animation/AnimNodeBase.h"
#include "ActiveRagdollAnimNode.generated.h"

USTRUCT(BlueprintType)
struct FAnimNode_ActiveRagdoll : public FAnimNode_Base
{
 GENERATED_USTRUCT_BODY()

 UPROPERTY(EditAnywhere, BlueprintReadWrite, Category = Links)
 FComponentSpacePoseLink mBasePose;

 UPROPERTY( EditAnywhere, BlueprintReadWrite, Category = Links, meta = (PinShownByDefault) )
 FRotator mInitialRelativeRotation;

 UPROPERTY( EditAnywhere, BlueprintReadWrite, Category = Links, meta = (PinShownByDefault) )
 FVector mInitialRelativeTranslation;

 UPROPERTY( BlueprintReadWrite, EditAnywhere, Category = Links, meta = (PinShownByDefault) )
 float mTranslationWeight;

 UPROPERTY( BlueprintReadWrite, EditAnywhere, Category = Links, meta = (PinShownByDefault) )
 float mRotationWeight;

protected:
 float mDeltaTime;

public:
 /************/
 FAnimNode_ActiveRagdoll();

 /****************************************************************/
 void Initialize_AnyThread( const FAnimationInitializeContext& Context ) override;

 /****************************************************************/
 void Update_AnyThread( const FAnimationUpdateContext& Context ) override;

/****************************************************************/
void CacheBones_AnyThread( const FAnimationCacheBonesContext& Context ) override;

 /*********************************************************/
 void EvaluateComponentSpace_AnyThread( FComponentSpacePoseContext& Output ) override;
};


UCLASS(BlueprintType)
class ANIMBASEDRAGDOLL_API UAnimGraphNode_ActiveRagdoll : public UAnimGraphNode_Base
{
 GENERATED_BODY()
 
public:
 UPROPERTY(EditAnywhere, Category = Links)
 FAnimNode_ActiveRagdoll mAnimPose;

 virtual FText GetNodeTitle(ENodeTitleType::Type TitleType) const override;
 virtual FLinearColor GetNodeTitleColor() const override;
 virtual FString GetNodeCategory() const override;
 virtual void CreateOutputPins() override;
};

CPP here:

#include "AnimBasedRagdoll.h"
#include "ActiveRagdollAnimNode.h"
#include "AnimationGraphSchema.h"
#include "AnimInstanceProxy.h"
#include "PhysicsEngine/PhysicsAsset.h"
#include "Components/SkeletalMeshComponent.h"

#define ANIM_MATH_PI 3.141592724f

//*******FAnimPoseNode implmentations*******************
FAnimNode_ActiveRagdoll::FAnimNode_ActiveRagdoll()
{
 mInitialRelativeRotation = FRotator( 0.f, 0.f, 0.f );
 mInitialRelativeTranslation = FVector::ZeroVector;
}


/*********************************************************/
void FAnimNode_ActiveRagdoll::Initialize_AnyThread( const FAnimationInitializeContext& Context )
{
 mBasePose.Initialize( Context );
};

/****************************************************************/
void FAnimNode_ActiveRagdoll::Update_AnyThread( const FAnimationUpdateContext& Context )
{
 mBasePose.Update( Context );
 mDeltaTime = Context.GetDeltaTime();
}

/****************************************************************/
void FAnimNode_ActiveRagdoll::CacheBones_AnyThread( const FAnimationCacheBonesContext& Context )
{
 mBasePose.CacheBones( Context );
}

/****************************************************************/
void FAnimNode_ActiveRagdoll::EvaluateComponentSpace_AnyThread( FComponentSpacePoseContext& Output )
{
 mBasePose.EvaluateComponentSpace( Output );
 
 const UAnimInstance* const lAnimInstance = Cast< UAnimInstance >( Output.AnimInstanceProxy->GetAnimInstanceObject() );
 USkeletalMeshComponent* lSkel = lAnimInstance->GetOwningComponent();

 if( lSkel && lSkel->IsSimulatingPhysics() )
 {
  FQuat lBoneQuaternion;
  FQuat lOwnerRotation;
  
  FVector lBoneTranslation;
  FVector lOwnerTranslation;

  const AActor* const lCharOwner = lAnimInstance->GetOwningActor();
  const UINT32 lPhysicsBoneCount = lSkel->GetPhysicsAsset()->SkeletalBodySetups.Num();
  
  if( lCharOwner )
  {
   lOwnerRotation = lCharOwner->GetActorRotation().Quaternion();
   lOwnerTranslation = lCharOwner->GetActorLocation();
  }
  else
  {
   lOwnerRotation = FQuat::Identity;
   lOwnerTranslation = FVector::ZeroVector;
  }

  for( uint8 i = 0; i < lPhysicsBoneCount; i++ )
  {
   const FName lBoneName = lSkel->GetPhysicsAsset()->SkeletalBodySetups[ i ]->BoneName;
   const FCompactPoseBoneIndex lInd( lSkel->GetBoneIndex( lBoneName ) );
   
   lBoneQuaternion = Output.Pose.GetComponentSpaceTransform( lInd ).GetRotation();
   lBoneTranslation = Output.Pose.GetComponentSpaceTransform( lInd ).GetLocation();

   //Setting up Linear Velocity

   // Updating bone positions in world space
   if( mTranslationWeight > 0.f )
   {
    const FVector lTargetPositionInWorld = lOwnerTranslation + lOwnerRotation *(
     (mInitialRelativeTranslation + mInitialRelativeRotation.Quaternion() * lBoneTranslation));

    FVector finalVelocity = (lTargetPositionInWorld - lSkel->GetBoneLocation( lBoneName )) / mDeltaTime;

    if( mTranslationWeight < 1.0f )
    {
     finalVelocity = FMath::Lerp( FVector::ZeroVector, finalVelocity, mTranslationWeight );
    }

    lSkel->SetPhysicsLinearVelocity( finalVelocity, false, lBoneName );
   }


   //Setting up angular velocity
   if( mRotationWeight > 0.f )
   {
    const FQuat lTargetRotationInWorld = lOwnerRotation * mInitialRelativeRotation.Quaternion() * lBoneQuaternion;
    const FQuat lRotDiff = lTargetRotationInWorld * lSkel->GetBoneQuaternion( lBoneName ).Inverse();
    const float lAngDiff = 2.0f * FMath::Acos( lRotDiff.W );
    FVector lAngVelocity;

    //Checking for shortest arc.
    if( lAngDiff < ANIM_MATH_PI )
    {
     lAngVelocity = lRotDiff.GetRotationAxis().GetSafeNormal() * lAngDiff / mDeltaTime;
    }
    else
    {
     lAngVelocity = -lRotDiff.GetRotationAxis().GetSafeNormal() * (2.0f * ANIM_MATH_PI - lAngDiff) / mDeltaTime;
    }

    if( mRotationWeight < 1.0f )
    {
     const FVector currentAngularVelNormalized = lSkel->GetPhysicsAngularVelocityInRadians( lBoneName ).GetSafeNormal();
     FQuat lInterpolatedRot = FQuat::FindBetweenVectors( currentAngularVelNormalized, lAngVelocity.GetSafeNormal() );
     lInterpolatedRot = FQuat::Slerp( FQuat::Identity, lInterpolatedRot, mRotationWeight );
     const float lRotRad = FMath::Lerp( 0.f, lAngVelocity.Size(), mRotationWeight );

     lAngVelocity = lAngVelocity.GetSafeNormal() * lRotRad;
    }

    lSkel->SetPhysicsAngularVelocityInRadians( lAngVelocity, false, lBoneName );
   }
  }
 }
}

/*******AnimGraphNode Implmentations. Codes Below Are Just Used for Unreal Editor. No Run-Time Code*******************


/******************Title Color!****************************/
FLinearColor UAnimGraphNode_ActiveRagdoll::GetNodeTitleColor() const
{
 return FLinearColor(0, 12.0f, 12.0f, 1.0f);
}

/***************Node Category***********************/
FString UAnimGraphNode_ActiveRagdoll::GetNodeCategory() const
{
 return FString("Active Ragdoll");
}

/*******************************Node Title************************************/
FText UAnimGraphNode_ActiveRagdoll::GetNodeTitle(ENodeTitleType::Type TitleType) const
{
 return FText::FromString("Move Physical Bones to Animation Pose");
}


/*******************************Exposing Output Pins************************************/
void UAnimGraphNode_ActiveRagdoll::CreateOutputPins()
{
 const UAnimationGraphSchema* Schema = GetDefault();
 CreatePin( EGPD_Output, Schema->PC_Struct, TEXT( "" ), FComponentSpacePoseLink::StaticStruct(), /*bIsArray=*/ false, /*bIsReference=*/ false, TEXT( "Pose" ) );
}

As you can see there are weight values for both angular and linear velocity. If these weights are set to 1.0, the physics will follow the animation pose 100%. So I suggest to change these two weight values based on gameplay events. For example if the character gets hit by an explosion the weights can be set to zero so we can have pure ragdoll simulation and after a while based on the average linear speed of the skeletal mesh (or it's pelvis velocity), you can increase the value until it gets to 1.0 and afterwards you can blend back to animation and turn off simulation. Simulation should be turned on when it's needed because it can be an expensive procedure.

And here are some GIFs out of the results:

GIF above shows the character with 100% angular velocity adjustment applied and zero percent of linear velocity. As you can see the character follows joint rotations while responding to external forces.

GIF above shows the character with 50% angular velocity adjustment  applied and zero percent of linear velocity. As you can see the character follows joint rotations but not completely!

GIF above shows the character with 10% angular velocity applied and zero percent of linear velocity. As you can see the character has a loose pose but still carries some percentage of animation pose.

GIF above shows the character with 100% angular and linear velocity applied. As it's shown, character saves its animated form completely with  both bones positions and rotations but the responses to external forces look like a glitch!

GIF above shows the character with 30% angular and linear velocity applied. As It's shown in the GIF, character saves its animated form partially but the response to external forces is smoother now!

Results above shows these weights should be controlled externally based on the gameplay events to let the character have a natural physical pose based on the context of gameplay.


Alternative Approach Using Spring Dampers

There is also an alternative approach to make active ragdoll happening. So instead of directly setting the angular and linear velocity of the bones we can apply a desired torque or force to make them following the animation pose. This approach uses a spring-damper equation to move the bones toward the animation pose. Here, the animation pose is considered as equilibrium point for the system. First we see how far the bone is from its equilibrium point then we apply a torque which can move the bone toward the point (Spring). Then there is resistant angular velocity which is applied in the opposite direction of the bone to smooth out the movement (damper) and avoid oscillation as much as possible.

The torque applied to each bone is calculated with this equation:

Joint_Torque = k * ( joint_rotation_from_animation * Inverse( current_joint_rotation ) ).RotaionAxis - m *  joint_angular_velocity; //rotations are in quaternions and in world space.


As you can see there are two gain values involved in this equation and you need to set them manually. These gains are used to scale the effect of spring and dampness for the movement. These gains should be different from joint to joint based on their mass and their momentum! The problem with this approach is that we need to do a lot of trial and error to set these gain values for each bone to avoid crazy oscillation but it also has pros as well. It can make smoother external physical reactions because we're not force setting the velocities directly and just trying to apply torques and forces toward the target so the bones can carry their current pure momentum.

However the famous paper below suggests an inertia scaled method for joints where all the bone gains are scaled automatically based on their parent bone's angular momentum. With this, specifying the gains can be done with less trial and error but still needs consideration.

ZORDAN, V. B., AND HODGINS, J. K. 2002. Motion capturedrivensimulations that hit and react. In ACM SIGGRAPH / EurographicsSymposium on Computer Animation, 89–96. 

Using Multiple Bones to Look At a Target in World Space.

This post explains the details of a plugin I created for Unity3D. The plugin is about to have characters looking at a target in a biomechanically correct way and using more than one bone to look at a target in world space. The plugin can be found from asset store via link below:

http://u3d.as/136L

The post is organized as follows. First, the workflow of the plugin is completely explained to help users understand the topic well. Also the blog post tries to carry an academic approach so if anyone wants to implement this feature on another platform can get an idea how to do it. Second the API and parameters of the plugin is explained so users know exactly how to use the system and at the end, important notes are provided. Make sure to completely read the section "important notes on setting up" if you don't have time to read the whole documentation.

1- Introduction

Imagine you want to write something using your computer's keyboard. When you are pressing keyboard buttons, you are mostly using your fingers and less movement comes from your arms or elbows. This shows a simple and basic rule in biomechanics, telling that if you can use your small muscles to do something, you will use them and you won't involve your big muscles in action. Using bigger muscles means consuming more energy and it's avoided on unnecessary situations. Of course using small muscles always need more focus and training. That's why you see a kid can start walking between age 1 or 2 but he can't tie his shoe laces until a reasonable age.

So let's consider another example. A pull up action. When you want to pull up your weight using a pull up bar first you use fingers to hang, then you see your fingers' tendons, ligaments and muscles are stretched and they can't hold your weight then you use your elbow and you see your elbow muscles are extended and tendons are getting stretched then you add your arms to the action and this procedure continues for your shoulders, chest and abs' muscles. So as you can see, you tried to do the action first with your small muscles and since they weren't powerful enough, you asked for help from your other muscles and managed to use your bigger muscles to finish the action.

Now let's expand this on another example. A look at example! So now imagine there is a picture in front of you. You can look at it without moving your head and just by moving your eyes. Now move the picture a few centimeters to your left. You still can look at the picture with your eyes however you feel your eyes muscles are getting stretched and tired. Now again move it a bit more to left you. Try to look at it and you see you can't look at the picture with just using your eyes because your eyes muscles are stretched completely and the picture is out of your eyes joint range so you need to use your neck and head as well to look at the picture. So continue like this and move the picture away from you and even more toward your back. You will see your head and neck joints and muscles get stretched and you need to rotate your spine and chest joints to look at the target. At the end you see that all your eyes muscles, head, neck and spine are in action to let you look at the target just like the pull up example where you couldn't just use your finger muscles to pull up your weight and lots of other muscles came into action for you to pull your weight up.

Perfect look at is working based on this rule. In perfect look at, you can define a chain of bones and their corresponding joint limits in degrees. If the first joint reaches its limit the second one starts rotating to look at the target. When the second bone reaches its limit the third one starts rotating and this procedure goes until the end of the bone chain. This way you can create a combination of bones to look at a target and not just use simple head movement. Let's have look at the results in these videos:

2- Technical Workflow

This section describes the look at procedure with details.

Every defined bone in look at bone chain has a forward vector which is used to show the bone's current direction. A target in world space is defined as the point which character wants to look at. To look at the point, the system starts from the first bone in the chain. It gets the current bone's forward vector and then calculates the rotation which can bring the bone's forward vector to the difference vector of the target point and the bone position in world space. Pic below shows the vectors.

The first bone rotates and will be clamped into its joint limit range. If the first bone meets its joint limit the second bone starts to rotate to let the first bone follow the target. Please note that the second bone should be an ancestor of the first bone. It should not be necessarily its parent but a bone in the same hierarchy which can rotate the first bone when it rotates. The same relation should go for bone two, three and so on. For example if the first bone is head, the second bone can be neck or chest because they are ancestors of the head but it can't be eye because eye is not an ancestor of head.

To rotate the next bone in the bone chain, the system needs to specify a forward vector and a target vector to find the rotation between them. The forward vector is calculated by adding the normalized rotated forward vector of the first bone and the position differences of the first bone of the chain to the current bone( all in world space ).

The target vector is calculated by adding the position difference vector from the first bone of the chain to the current bone and adding this to the normalized position difference vector of target point from the first bone position. This way, by rotating next bones in the look at at chain, we can make sure the first bone in the chain aligns to the target even if the target is out of its joint range. Just a small note here, if the first bone has a huge translation difference from the next bones in the look at chain, the final look at result might have a little error and it won't exactly meet the target but generally character will always look at the target with a good precision which can provide a good intuition of character look ats.

The same workflow continues until the first bone can hit the target or the final bone in the chain meets its joint limit.

Each joint limit is calculated based on the angle between its forward vector and its parent's forward vector. By parent I mean the exact parent in the skeleton hierarchy however the joint angle limit can be calculated easier by calculating the difference of the current bone rotation with its corresponding reference pose rotation but unfortunately Unity Mecanim is not exposing the reference pose into scripts and currently there is no way getting the reference pose. Whenever unity exposes the reference pose into the scripts, both the bone forward vector and parent forward vector will be removed and the reference pose forward vector will be used instead to provide an easier setup for users.

3- Perfect Look At Component Properties

Up Vector:

Up vector shows the character’s world yaw axis which is set to engine’s up axis by default. This vector is used as an axis for “Rotate Around Up Vector Weight”. When “Rotate Around Up Vector Weight” is set to one the bone just rotates around up vector and for any values less than one, the axis blends between the original rotation axis and the up vector axis.

Target Object:

A game object used as the target object for the system. Characters with perfect look at component will look at this object.

Look At Blend Speed:

This value shows how fast the current look at pose will be blended in from the last look at pose. This smooth blending can be very helpful specially when look at is applied on top of a dynamic animation which has a lot of movement.

Leg Stabilizer Min Distance To Start Solving:

This value is used for leg stabilizer feature. If the difference between feet bone before and after applying perfect look at is more than this value the system tries to fix the feet to avoid any foot sliding. The difference is more than zero if any of the parent bones of the “foot bone” changes rotation by perfect look at. If you set this value to a high value it can cause jitters on legs. If the value is zero the leg stabilizer is always called. It’s recommended not to change this value from its default unless it’s needed.

Please check the Leg Stabilizers section to find out more about the feature.

Leg Stabilizer Max Iterations:

Leg stabilizer uses FABRIK IK solver to avoid feet sliding. This value shows the maximum number of iterations to solve the IK solution. It’s recommended not to change this value from its default if your character has 3 or 4 leg joints. For character more than 4 leg joints the recommended value is 30.

Please check the Leg Stabilizers section to find out more about the feature.

Draw Debug Look At:

If checked, target vectors and forward vectors for each bone is drawn in scene viewport. Target vectors are drawn in red and forward vectors are green.

Look At Bones:

An array of look at bone data. The size of the array should be equal to the number of bones you want to get involved in the look at process. Make sure there would be no missing bone in the array unless the systems prevent itself from working.

Bone:

The look at bone which is going to be rotated to look at the target.

Rotation Limit:

Joint limit in degrees. If the angle difference between the current bone and its parent in the skeleton hierarchy is higher than this value the next bone in the "Look At Bones" array starts rotating to help the first bone reach the target.

Rotate Around Up Vector Weight:

This value shows how much a rotation should be toward character up vector. This value can be very useful for bones which has higher rank in the look at chain hierarchy for example spine bones. When Rotate Around Up Vector Weight is set to zero for a spine bone in a look at chain, the spine bone can be rotated in three directions while a human doesn’t usually rotate the spine in three dimensions to look at a target. Two pics below can show the differences:




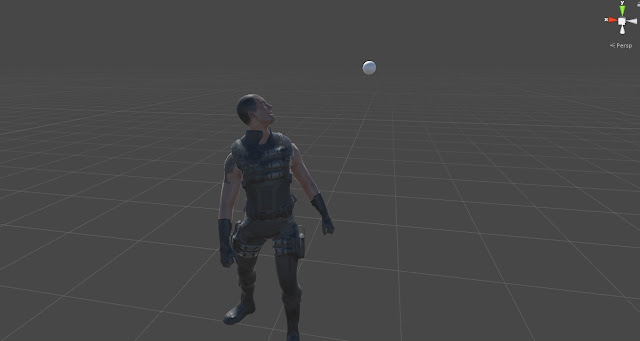
Pic above shows the character while the values for the Rotate Around Up Vector Weight is set to zero for all the bones. As you can see the spine has some extra rotations which is not quite natural. When a humanoid wants to look at a target it mostly rotates its spine in yaw axis and less in pitch and roll. This limited rotation is done to be sure the body remains balanced because spine carries a big part of upper body mass and by rotating it, the body center of mass can be changed and the character loses balance so setting this value for spine bones can help to achieve a more natural pose.


In Pic below values for the Rotate Around Up Vector is set as follows:

Eyes: 0
Head: 0
Neck: 0
Spine1: 0.1
Spine2: 0.2
Spine3: 0.7



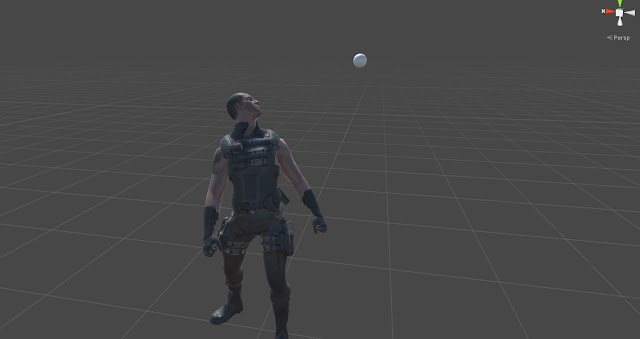
As you see in the results, the spine rotations are more natural now. To find out examples of this case please check out the three provided prefabs in the project.

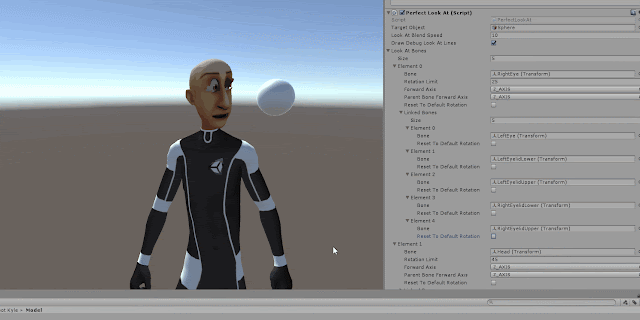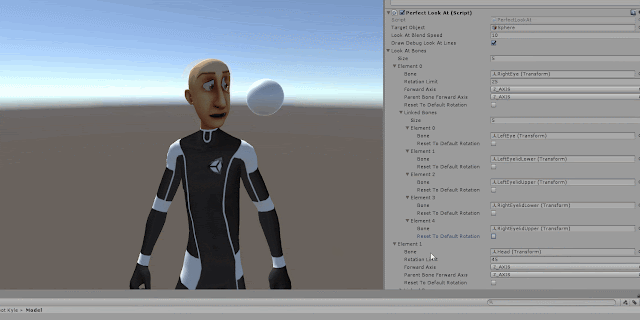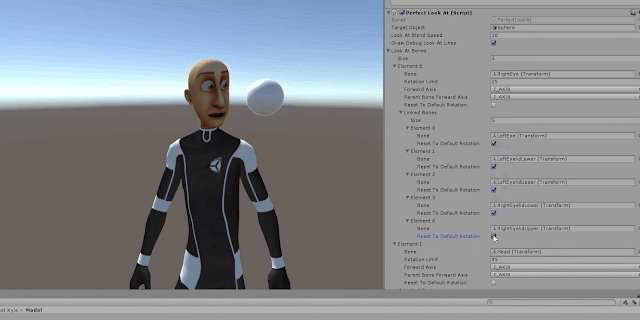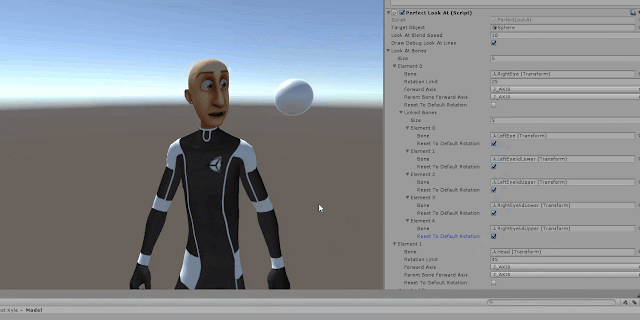
Forward Axis:

The forward vector of the bone. To find the forward axis of a bone, first you need to turn the coordinate system into local then you need to select the bone from the hierarchy panel. Afterwards you can find the forward vector. Picture below shows an example how to find the forward vector of the head bone for a character. As you can see the forward vector for this bone is Y-Axis:

Parent Bone Forward Axis:

The forward vector of the current bone's parent. To find the forward axis of the parent bone first you need to turn the coordinate system into local then you need to select the bone's parent from the hierarchy panel. Afterwards you can find the forward vector. Picture below shows an example how to find the forward vector of the head's parent bone which in this case is neck. As you can see the pic below, neck's forward vector is Y-Axis:

Reset To Default Rotation:

In Unity Mecanim, when an animation is retargetted on a different rig, if that rig has more bones than the retargetted animation, those bones never get updated to any specific transform. This mean they always use a cached value of the last valid transformation they already received and the pose buffer never gets flushed which sometimes makes problems. To avoid having this situation, make sure to check the "Reset to Default Rotation". Check this check box only when you are sure the look at bones don't receive any pose from the current animation otherwise leave this check box unchecked. Check out the two GIFs below to find out the differences:

As you can see in the GIF above the spine remains disconnected because it receives no pose from animation and it uses the last valid cached pose. By checking the Reset To Default check box we can create a valid rotation for the bones which don't have any animation but want to be in the look at bone chain.

Linked Bones:

Linked bones are the bones which should be rotated as same as the current bone. For example, one look at bone chain can be created like this:

Lookat Bone 1 = Right Eye

Lookat Bone 2 = Head

Lookat Bone 3 = Neck

Lookat Bone 4 = Spine2

Lookat Bone 5 = Spine1

Lookat Bone 6 = Spine0

As you can see, there is no Left eye here. So if you apply this look at bones chain to the character, all the bones can be rotated based on their joint limits but the left eye remains still. Here we can define left eye as a linked bone of the right eye. So wherever right eye rotates, left eye also rotates with it. Just like a linked transform. You can add as many as linked bone you want to the current bone.

To find examples of linked bones check out HumanCharacter and UnityCharacter prefabs in the project.

Linked Bones-Reset to Default Rotation:

This is exactly the same as Reset To Default Rotation in the LookAtBones. If you face some situations like the GIF below when you add linked bones, this means the linked bone doesn't carry any animation info and you need to check the Reset To Default Rotation for the bone to make the Mecanim pose buffer not to use the invalid poses.

Leg Stabilizers:

If there is a bone in chain of look at bones which is the parent of legs, then by rotating that bone the legs can slide on the ground. For example in a humanoid character you can set these bones for look at chain: eyes, head, neck, spine2, spine1 and pelvis. Since the pelvis is the parent of thighs by rotating it the legs start rotating and the feet start sliding on ground. This issue can be avoided by setting leg stabilizer. Leg stabilizer set the feet and knee exactly like original animation so rotating the pelvis won’t slide the legs and won’t twist the knees. This feature can be useful for quadruped characters as well. The feature fixes the knee angle and feet position based on original animation to save the fidelity to original movement.

As an example, please check out Human and Unity Character prefabs in the project.

Foot Bone:

The bone that needs to be stabilized when one of its parents are rotated by perfect look at. It usually is the foot bone. This will be the end effector of the IK chain defined by leg stabilizer.

As an example, please check out Human and Unity Character prefabs in the project.

IK Weight:

If this value is set to 1, the selected bone will be completely constrained to IK and get stabilized completely. If set to, it 0 will be completely free from IK and no feet stabilization happens. Any value between 0 and 1 makes an average out of stabilized IK feet and free FK feet. You might need to change the weight value based on some gameplay events. For example there is no need to stabilize feet when the character is falling so the weight can be set to zero in such a case.

Bones Count:

The number of bones to be added to the Leg stabilizer IK chain. For example for a biped character it should be 3. The first bone is the foot bone which already set in the foot bone slot, second is the calf and the third is the thigh. The system automatically gets the parents of the Foot Bone and add them to the IK solver.

As an example, please check out Human and Unity Character prefabs in the project.

4- Perfect Look At Component Public API:

GetLookAtWeight():

Returns the current weight of the perfect look at. If weight is zero, perfect look at is turned off, if one perfect look at is applied 100% and any value between will make an average between animation and procedural rotation provided by perfect look at.

SetLookAtWeight( float weight ):

Sets the current weight of the perfect look at. Please note if you use this function any transition will be cancelled because Perfect Look At is not letting external systems to change the weight in two different ways. By two different ways I mean setting look at weight manually or by calling Enable/DisablePerfectLookAt.

This cancelling is provided to avoid having an error-prone pipeline. To find out more about transitions, check out EnablePerfectLookAt and DisablePerfectLookAt.

EnablePerfectLookAt( float time, bool cancelCurrentTransition = true ):

If this function is called, perfect look at's weight will turn into one within the specified time (blending in).

cancelCurrentTransition: If set to true and if another call to this function or DisablePerfectLookAt is made and the system is still on the transition, the current transition time will be set to zero and transition will continue from current weight to the destination weight within the new time specified.

If cancelCurrentTransition is false and if the system is on a transition, any other call to DisablePefrectLookAt or EnablePerfectLookAt will be ignored.

DisablePerfectLookAt( float time, bool cancelCurrentTransition = true ):

If this function is called, perfect look at's weight will turn into zero within the specified time. All other details are the same as EnablePerfectLookAt. Please refer to EnablePerfectLookAt to find out more about the function parameters.

IsInTransition():

If PerfectLookAt is on disabling or enabling transition, it will return true otherwise false.

GetTimeToFinishTransition():

If PerfectLookAt is on disabling or enabling transition, it returns the remaining time to finish transition.

Important Notes on Setting up Perfect Look At:

Perfect Look At is a component. To use it, it's just needed to be assigned to a game object. Some important cases to use Perfect Look At is addressed here:

1- Turn Off Optimize Game Objects:

The only way to change bones transformations in a procedural way in Unity, is through LateUpdate of a component. Unfortunately Unity won't let you set the bones transforms if the "Optimize Game Objects" option of a rig is checked. To make PerfectLookAt working you need to be sure "Optimize Game Objects" is not checked. There is no info on Unity documentation why it is impossible to transform bones in an optimized rig and how Unity Optimize the skeleton calculations.

2- Setting Reset To Default Rotation On Some Necessary Cases:

If you see any of the linked bones are rotating constantly make sure you turn the Linked Bone's Reset To Default Rotation on. To find out more why this issue is happening please refer to Reset To Default Rotation section in this documentation.

3- Defining the Forward Axis of The Bones and Their Corresponding Parents Correctly:

Make sure you always select the correct forward axis both for the bone and its parent. Make sure you change the coordinate system to local and see the bone and its parent's forward axis in the local coordinate system. For more info please check out "Forward Axis" and "Parent Bone Forward Axis" section in this document. 

4- Look At Bones Should Be In The Same Hierarchy But Not Necessarily Child and Parent:

Look at bones order in the "Look At Bones" array matters. It should be set based on the bones hierarchy. For example 4 bones( two eyes, head and chest ) are needed to rotate using perfect look at. These 4 bones should be specified in this order:

First Bone: Left eye ( its linked bone should be right eye )

Second Bone: Head

Third Bone: Chest

As you can see, bones defined here are not necessarily parent and child but they are in the same hierarchy. For example Chest is the parent of neck and neck is the parent of head. So when Chest rotates, head will also rotates.

5- Checking Character Prefabs as an Example:

Make sure to check the 3 Prefab Characters and their corresponding scenes as an example of perfect look at. All 3 have different rigs and they use perfect look at. They can be found in Assets/Media/Prefabs