Have you ever tried to animate a character's bone with a simple rotation along one of the world axis but you see a weird interpolation? An ugly interpolation in two or three axis instead of one! For sure this wasn't what you were expecting. Let's check this GIF:
You rotate the box along X and set a keyframe for it but when you play the animation you will see the box is rotating along X and Y! Well, in this post I want to explain why this issue is happening!
Before going further, let's talk a little about Euler Angles. All the people in animation know this word because it's the most intuitive method for rotating objects in 3D space and rotation has the highest number of clicks within a process of making an animated character. So what is Euler angles then? Euler proved that every unique rotation in 3D space can be described by three rotations along three orthogonal axis. These three rotations are called pitch yaw and roll. Euler angles are famous in 3D animation because they are easy to understand and imagine but every flexibility and ease of use will come up by a cost.
As I wrote earlier, Euler proved that every rotation can be defined uniquely in 3D space but he never said that I will provide you a nice interpolation between two different Euler rotations. So just to find out why this is happening I need to go a bit into the underlying math of Euler angles.
A rotation defined with Euler Angles is composed of 3 different values. Each of which shows rotation along one of the orthogonal axis. Rotation around X axis has a specific rotation matrix as well as rotation along Y and Z so when we want to rotate an object around X then Y and then Z we just need to multiply these matrices:
Z_RotationMatrix * Y_RotationMatrix * X_RotationMatrix
This Euler rotation is called Euler_XYZ. That means you first rotate the object along X then Y and then Z. The important point here is that Euler rotations order matters. The result that Euler XZY provides is different than Euler XYZ even with the same values of pitch, yaw and roll and the reason is because matrix multiplication is not commutative. Euler XZY is calculated like this:
Euler_XZY Rotation = Y_RoationMatrix * Z_RotationMatrix * X_RotationMatrix
And of course the two formulas are different because matrix multiplication order is important.
So let's consider Euler_XYZ. When Y rotation matrix is applied after X rotation matrix, it means the X rotation transformation provide by X matrix is always in the Y rotation matrix's space. That means the first rotation is the child of second. Why? because first we rotate the coordinate system with X rotation matrix and then we rotate the result with Y rotation matrix meaning the whole Y rotation is applied to the first transformation which is X rotation in this case. So wherever Y Matrix takes the coordinate system, X transform is also going there just like a parent-child relationship. This coordinate system with three consecutive rotation matrices is called Gimbal. So Euler angles is always measured in Gimbal coordinates.
Here are some screenshots for you to see how Gimbal rotation react when you rotate an object. Imagine our Euler angles rotation controller order is XYZ which means if we give values of X= 35, Y= 45 and Z=50 (all in degrees), it will rotate the object first with 35 degrees around X then 45 around Y and at the end 50 around Z. So here you can find the rotation applied step by step and see how Gimbal axis are being changed:
X =0, Y=0, Z=0: Check out the three rotation axis, everything looks normal just like world axis:
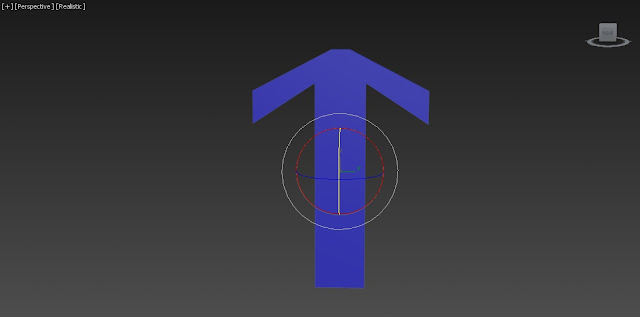
X=35, Y=0, Z=0: We rotated the object around X with 35 degrees. Again everything looks normal just similar to default world axis because X is the first rotation to be applied:

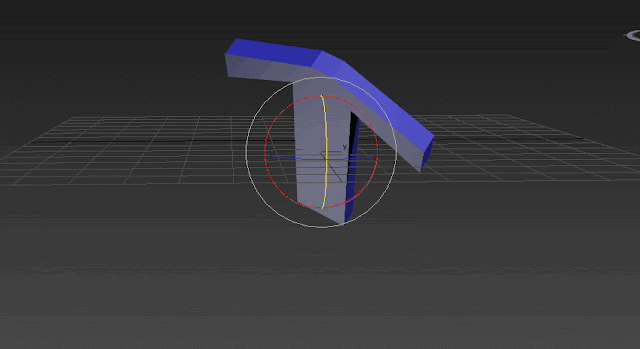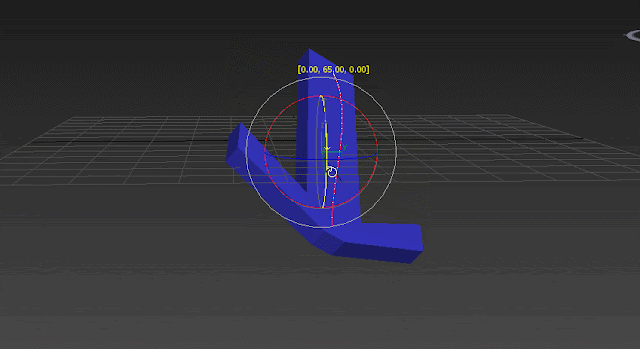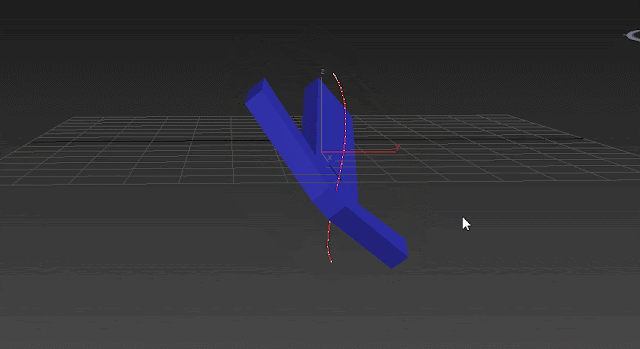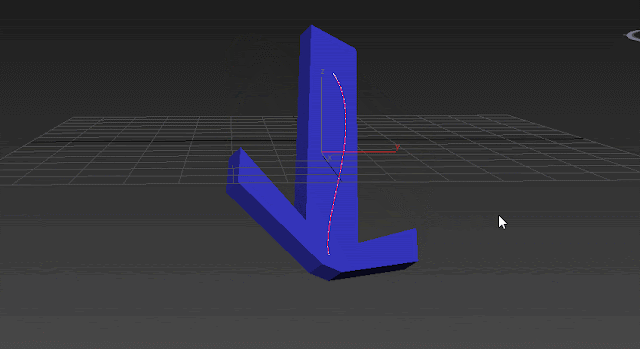
X=35, Y=45, Z=0. Y is rotated and you see the X axis is also rotated 45 degrees. Remember about the parent-child relationship I mentioned a few lines above. Here you can see it.

X=35, Y=45, Z=50. Z rotates 50 degrees and both X and Y rotate 50 degrees because in Euler XYZ, Z is the parent of all and all axis follow it:

So these are the axis you have after this rotation. Now imagine if you need to rotate the object in world Y axis again. Since Euler angles are defined in Gimbal coordinate system you can not achieve a rotation around world Y just by rotating the object in one axis. In this case to achieve a rotation around world Y axis, two or three axis will be rotating to be sure you will reach the specified rotation. So YES! here is the ugly and unexpected interpolation. You moved the object in one world axis but the object rotate itself in three or two different dimensions to reach the desired rotation:
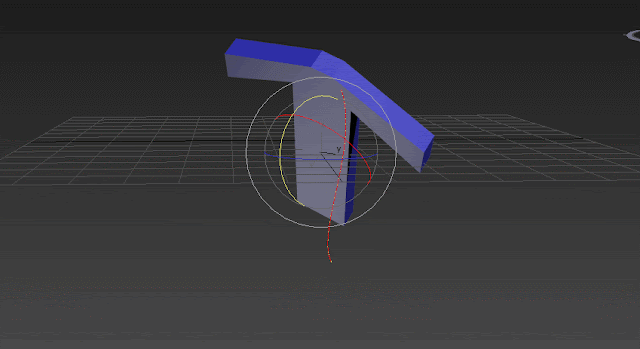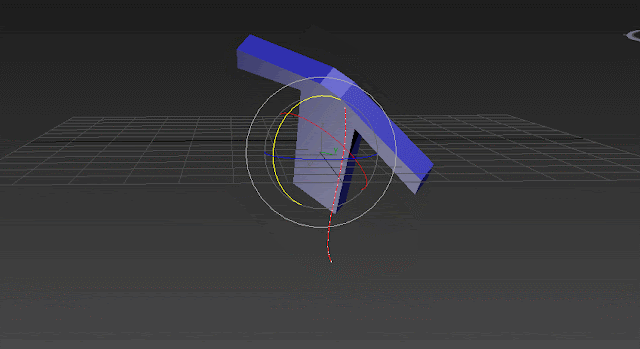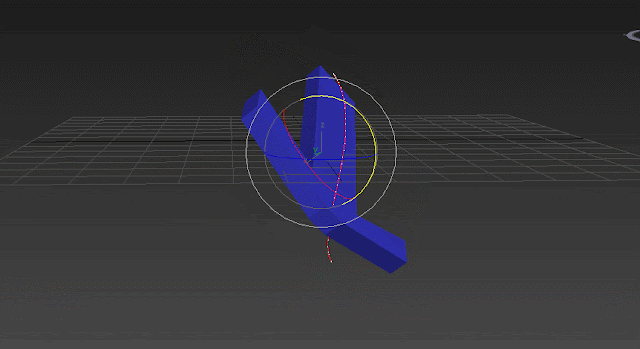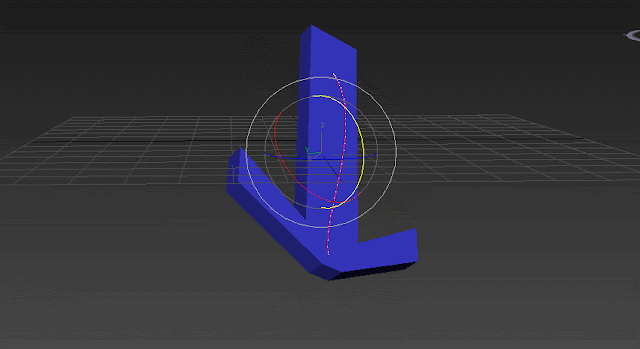
The trajectory above, shows how the object moves on an inefficient arc and it's not just rotation around Y. In the GIF above you can see 2 Gimbal axis are moving during the second rotation we applied (80 degrees around world Y axis):
So how can you avoid this unexpected interpolations while rotating bones or objects? One way is to always have an eye on Gimbal coordinate system. Don't let the World or Local reference coordinate system trick you. Local and World coordinate axis are just there to give a better intuition to the user but your mathematical reference coordinate system is Gimbal here. You can switch to Gimbal constantly to see how you can rotate the bones with less changes in different axis however Gimbal coordinate system suffers from an issue named Gimbal lock where you lose one degree of freedom and it can happen when you rotate second axis 90 degrees. For instance in the order of Euler XYZ if you rotate Y in 90 degrees then X will be aligned on Z because in Gimbal coordinate system X is the child of Y and by rotating Y with 90 degrees, X will rotate 90 degrees around Y as well and it will be aligned on Z. Check out the GIF below:
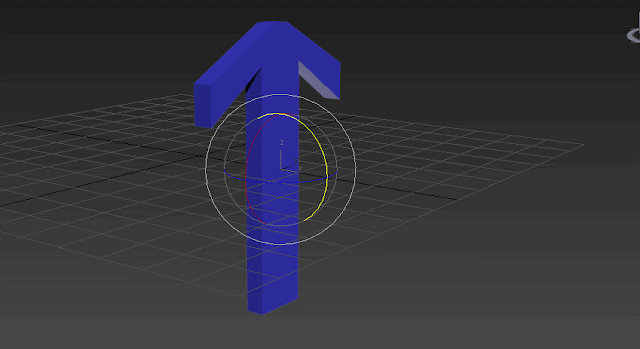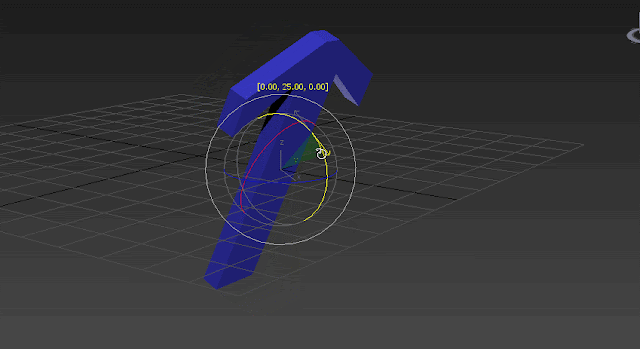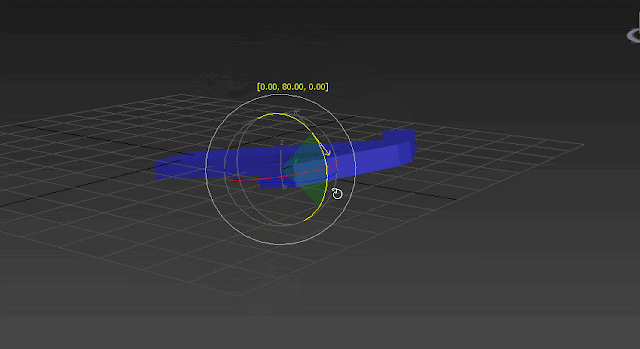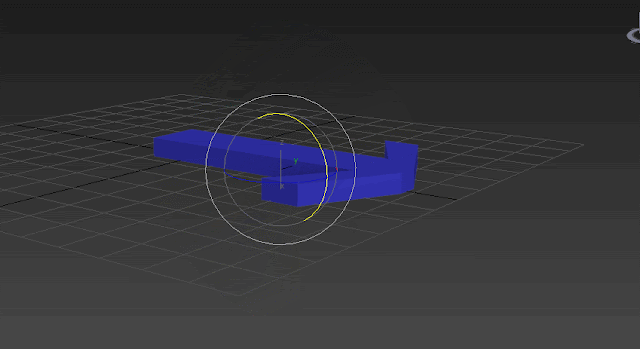
Now if you want to rotate the object in X axis for the next keyframe, there is no X anymore. Z and X are aligned together and you missed one degree of freedom as you can see in the GIF above. So to unlock the Gimbal lock you need to rotate the object in more than one axis again!
There is also another way to avoid bad interpolation and it's using unit Quaternion rotations instead of Euler angles. Quaternion SLERP interpolation can be very soft and smooth and it always act as expected since it selects the shortest arc possible from one rotation to another. The problem with Quaternions is that they are not intuitive enough to be presented by Bezier curves. The curves animators like so much and can have controls over it a lot! Quaternions are following a different kind of algebra and artists are not really enthusiastic to learn the math behind Quaternions and without learning the math, a Quaternion value can be very confusing however Quaternion rotation controller are still being used in DCC tools like 3DSMax and they come up with interpolators like TCB interpolators which can provide a very smooth interpolation between rotations. So rarely you need to change the TCB values and you can simulate the ease in/outs just by adding one or two single key frames. The only thing here is that you don't have control over the rotation of different axis because you just control the SLERP interpolation factor using a TCB curve and this factor is just a normalized value showing the interpolation percentage between two Quaternions using SLERP function.
When I was teaching game animation, I tried to teach my students to always use Quaternion controllers with TCB interpolators. Using Quaternion controllers with TCB interpolators gives you less control over the interpolation but when you use Quaternion interpolation it always uses SLERP function which selects the shortest arc from the source rotation to the destination. This means you can create your desired curve by just adding a little number of more keyframes and without frequently tweaking unexpected changes on curve values like what Euler angles interpolation offers. In next posts I will try to show you how you can have a better interpolation by using Quaternions instead of Euler angles and by just adding one or two extra key frames.
At the end, the case we studied above can turn to something like this when we switch the rotation controller from Euler XYZ to TCB Quaternion SLERP. As you can see the trajectory is very smooth and just follows the Y rotation in the world. You can compare the trajectories in two GIFs to see the differences!
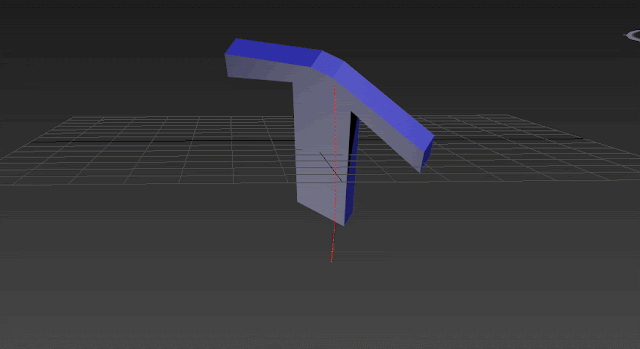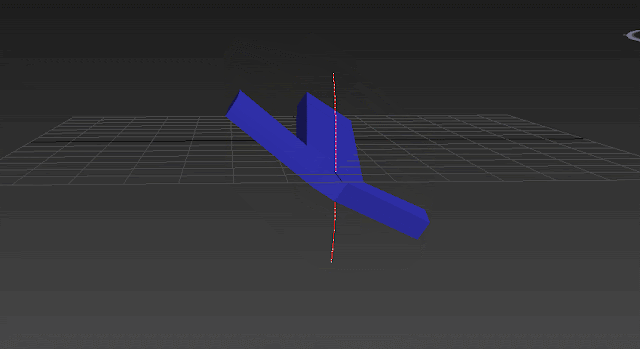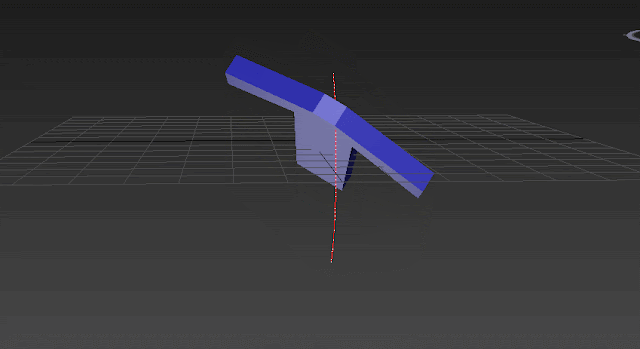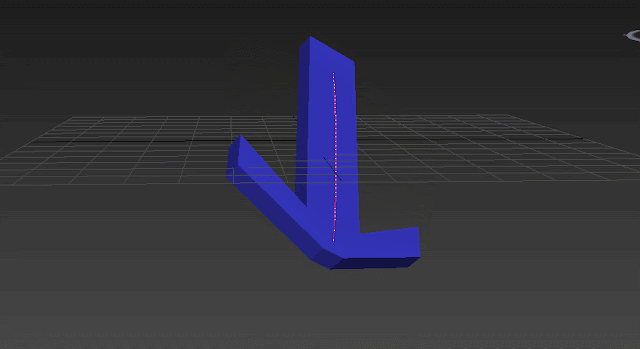
You rotate the box along X and set a keyframe for it but when you play the animation you will see the box is rotating along X and Y! Well, in this post I want to explain why this issue is happening!
Before going further, let's talk a little about Euler Angles. All the people in animation know this word because it's the most intuitive method for rotating objects in 3D space and rotation has the highest number of clicks within a process of making an animated character. So what is Euler angles then? Euler proved that every unique rotation in 3D space can be described by three rotations along three orthogonal axis. These three rotations are called pitch yaw and roll. Euler angles are famous in 3D animation because they are easy to understand and imagine but every flexibility and ease of use will come up by a cost.
As I wrote earlier, Euler proved that every rotation can be defined uniquely in 3D space but he never said that I will provide you a nice interpolation between two different Euler rotations. So just to find out why this is happening I need to go a bit into the underlying math of Euler angles.
A rotation defined with Euler Angles is composed of 3 different values. Each of which shows rotation along one of the orthogonal axis. Rotation around X axis has a specific rotation matrix as well as rotation along Y and Z so when we want to rotate an object around X then Y and then Z we just need to multiply these matrices:
Z_RotationMatrix * Y_RotationMatrix * X_RotationMatrix
This Euler rotation is called Euler_XYZ. That means you first rotate the object along X then Y and then Z. The important point here is that Euler rotations order matters. The result that Euler XZY provides is different than Euler XYZ even with the same values of pitch, yaw and roll and the reason is because matrix multiplication is not commutative. Euler XZY is calculated like this:
Euler_XZY Rotation = Y_RoationMatrix * Z_RotationMatrix * X_RotationMatrix
And of course the two formulas are different because matrix multiplication order is important.
So let's consider Euler_XYZ. When Y rotation matrix is applied after X rotation matrix, it means the X rotation transformation provide by X matrix is always in the Y rotation matrix's space. That means the first rotation is the child of second. Why? because first we rotate the coordinate system with X rotation matrix and then we rotate the result with Y rotation matrix meaning the whole Y rotation is applied to the first transformation which is X rotation in this case. So wherever Y Matrix takes the coordinate system, X transform is also going there just like a parent-child relationship. This coordinate system with three consecutive rotation matrices is called Gimbal. So Euler angles is always measured in Gimbal coordinates.
Here are some screenshots for you to see how Gimbal rotation react when you rotate an object. Imagine our Euler angles rotation controller order is XYZ which means if we give values of X= 35, Y= 45 and Z=50 (all in degrees), it will rotate the object first with 35 degrees around X then 45 around Y and at the end 50 around Z. So here you can find the rotation applied step by step and see how Gimbal axis are being changed:
X =0, Y=0, Z=0: Check out the three rotation axis, everything looks normal just like world axis:

X=35, Y=0, Z=0: We rotated the object around X with 35 degrees. Again everything looks normal just similar to default world axis because X is the first rotation to be applied:

X=35, Y=45, Z=0. Y is rotated and you see the X axis is also rotated 45 degrees. Remember about the parent-child relationship I mentioned a few lines above. Here you can see it.

X=35, Y=45, Z=50. Z rotates 50 degrees and both X and Y rotate 50 degrees because in Euler XYZ, Z is the parent of all and all axis follow it:

So these are the axis you have after this rotation. Now imagine if you need to rotate the object in world Y axis again. Since Euler angles are defined in Gimbal coordinate system you can not achieve a rotation around world Y just by rotating the object in one axis. In this case to achieve a rotation around world Y axis, two or three axis will be rotating to be sure you will reach the specified rotation. So YES! here is the ugly and unexpected interpolation. You moved the object in one world axis but the object rotate itself in three or two different dimensions to reach the desired rotation:


The trajectory above, shows how the object moves on an inefficient arc and it's not just rotation around Y. In the GIF above you can see 2 Gimbal axis are moving during the second rotation we applied (80 degrees around world Y axis):
So how can you avoid this unexpected interpolations while rotating bones or objects? One way is to always have an eye on Gimbal coordinate system. Don't let the World or Local reference coordinate system trick you. Local and World coordinate axis are just there to give a better intuition to the user but your mathematical reference coordinate system is Gimbal here. You can switch to Gimbal constantly to see how you can rotate the bones with less changes in different axis however Gimbal coordinate system suffers from an issue named Gimbal lock where you lose one degree of freedom and it can happen when you rotate second axis 90 degrees. For instance in the order of Euler XYZ if you rotate Y in 90 degrees then X will be aligned on Z because in Gimbal coordinate system X is the child of Y and by rotating Y with 90 degrees, X will rotate 90 degrees around Y as well and it will be aligned on Z. Check out the GIF below:

Now if you want to rotate the object in X axis for the next keyframe, there is no X anymore. Z and X are aligned together and you missed one degree of freedom as you can see in the GIF above. So to unlock the Gimbal lock you need to rotate the object in more than one axis again!
There is also another way to avoid bad interpolation and it's using unit Quaternion rotations instead of Euler angles. Quaternion SLERP interpolation can be very soft and smooth and it always act as expected since it selects the shortest arc possible from one rotation to another. The problem with Quaternions is that they are not intuitive enough to be presented by Bezier curves. The curves animators like so much and can have controls over it a lot! Quaternions are following a different kind of algebra and artists are not really enthusiastic to learn the math behind Quaternions and without learning the math, a Quaternion value can be very confusing however Quaternion rotation controller are still being used in DCC tools like 3DSMax and they come up with interpolators like TCB interpolators which can provide a very smooth interpolation between rotations. So rarely you need to change the TCB values and you can simulate the ease in/outs just by adding one or two single key frames. The only thing here is that you don't have control over the rotation of different axis because you just control the SLERP interpolation factor using a TCB curve and this factor is just a normalized value showing the interpolation percentage between two Quaternions using SLERP function.
When I was teaching game animation, I tried to teach my students to always use Quaternion controllers with TCB interpolators. Using Quaternion controllers with TCB interpolators gives you less control over the interpolation but when you use Quaternion interpolation it always uses SLERP function which selects the shortest arc from the source rotation to the destination. This means you can create your desired curve by just adding a little number of more keyframes and without frequently tweaking unexpected changes on curve values like what Euler angles interpolation offers. In next posts I will try to show you how you can have a better interpolation by using Quaternions instead of Euler angles and by just adding one or two extra key frames.
At the end, the case we studied above can turn to something like this when we switch the rotation controller from Euler XYZ to TCB Quaternion SLERP. As you can see the trajectory is very smooth and just follows the Y rotation in the world. You can compare the trajectories in two GIFs to see the differences!

